Sieve of Eratosthenes

Given a number ‘n’, we need to print all the prime numbers up to ‘n’.

for(int i = 2; i * i <= n; i++)
{
    if(prime(i)) v.push_back(i);
}

This is the normal way to find primes up to ‘n’, but the time complexity of the above code is O(n * sqrt(n)), which takes a lot of time.
Therefore, we will use the Sieve of Eratosthenes algorithm for better time complexity.

How It Works

The algorithm works on a simple principle: any multiple of a prime number cannot be prime.
By systematically marking off these multiples, we are left with only prime numbers.

First, create a list of consecutive integers from 2 to ‘n’ (since 0 and 1 are not prime), then initialize them with 1 (assuming all numbers are prime initially).
For n = 30, the process looks like this:

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30

In this list, the first number is 2, which is the first prime number. Since any multiple of a prime can never be prime, we will mark off all the multiples of 2 up to 30.

1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0
2	3		5		7		9		11		13		15		17		19		21		23		25		27		29

Now the second number (and also the second prime) is 3. We will mark off all the multiples of 3 up to 30 in the same way.

1	1	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0
2	3		5		7				11		13				17		19				23		25				29

After 3, the next number is 4, but it’s not a prime number because it’s a multiple of 2. The multiples of 4 are also divisible by 2, so they were previously marked off by 2.
The next number is 5, and it’s a prime number. Therefore, we mark off all the multiples of 5.

1	1	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0	0	0	0	0	1	0
2	3		5		7				11		13				17						23						29

The next number is 6, which is a multiple of both 2 and 3, so it’s not a prime number. The multiples of 6 were already marked off by 2 or 3.
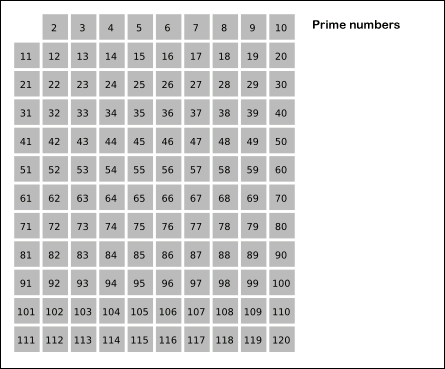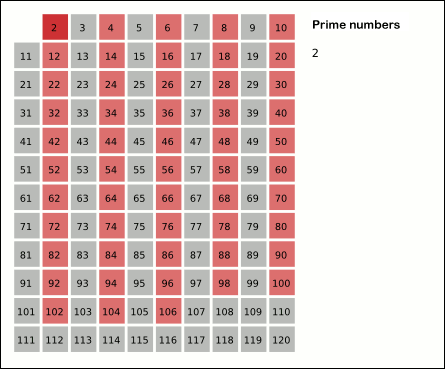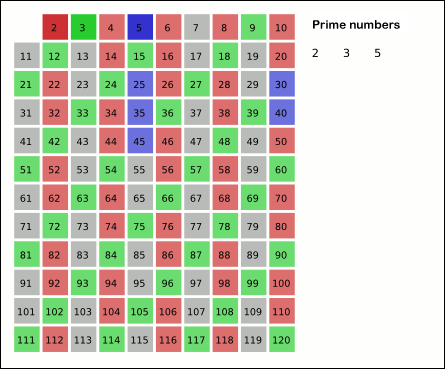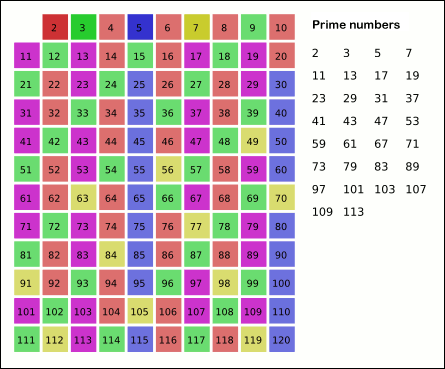
This marking off cycle repeats until all the multiples of each prime are marked off and only the primes up to ‘n’ remain in the list.
For n = 30, the final list looks like this:

1	1	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0	0	0	0	0	1	0
2	3		5		7				11		13				17						23						29

The prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.

Here is the code implementation of the Sieve of Eratosthenes algorithm:

#include <bits/stdc++.h>
using namespace std;

// function to find all prime numbers up to 'n'
vector<int> findAllPrimes(int n) {
    // initialize with 1 (assuming all numbers are prime initially)
    vector<int> prime(n + 1, 1);
    
    // 0 and 1 are not prime
    prime[0] = prime[1] = 0; 
    
    // apply Sieve of Eratosthenes
    for (int i = 2; i <= sqrt(n); ++i) {
        if (prime[i] == 1) {
            for (int j = i * i; j <= n; j += i) {
                // mark multiples of prime numbers as not prime
                prime[j] = 0; 
            }
        }
    }
    
    vector<int> ans;
    // collect prime numbers
    for (int i = 2; i <= n; ++i) 
    {
        if (prime[i] == 1) ans.push_back(i);
    }
    return ans;
}

int main() 
{
    int n = 30;
    vector<int> primes = findAllPrimes(n);

    cout << "Prime numbers less than or equal to " << n << ":" << endl;
    for (auto prime : primes) {
        cout << prime << " ";
    }
    cout << endl;

    return 0;
}

Time and Space Complexity for the Sieve of Eratosthenes algorithm:

Time Complexity = O(nlog(logn))
Space Complexity = O(n)

Here is an animated visualization of how the Sieve of Eratosthenes works, for n = 120: